隐性变量法的基本思路是,将全要素生产率视为一个隐性变量即未观测变量,从而借助状态空间模型(state space model) 利用极大似然估计给出全要素生产率估算。
隐性变量法的应用
具体估算中,为了避免出现伪回归,需要进行模型设定检验包括数据平稳性检验和协整检验。平稳性检验和协整检验的方法很多,常见的有ADF (the Augmented Dickey-Fuller) 单位根检验和JJ(Johanson and Juselius ,1990) 协整检验。由于产出、劳动力和资本存量数据的趋势成分通常是单位根过程且三者之间不存在协整关系,所以往往利用产出、劳动力和资本存量的一阶差分序列来建立回归方程。采用C - D 生产函数,且假设规模收益不变,则有如下观测方程:
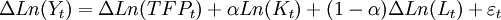(1)
其中,Δ L n( T F P t) 为全要素生产率增长率,假设其为一个隐性变量,且遵循一阶自回归即AR 过程,则有如下状态方程:
Δ L n( T F P t) = ρΔ L n( T F P t − 1) + υ t (2)
其中,ρ为自回归系数,满足| ρ| < 1 ,
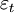为白噪声。这样,利用状态空间模型,通过极大似然估计同时估算出观测方程(1) 和状态方程(2) ,从而得到全要素生产率增长的估算值。隐性变量法的最大优点在于,不再将全要素生产率视为残差,而是将其视为一个独立的状态变量,这样将全要素生产率从残差中分离出来,从而剔除掉一些测算误差对全要素生产率估算的影响。同时,在具体估算时,还充分考虑了数据非平稳性带来的伪回归问题。
相关条目 全要素生产率分析代数指数法增长会计法
-
相关文章
刘霆龙12.10黄金走势空头能否延续
元宇宙到底是什么？这十点看完就明白了
蚂蚁链“粉丝粒”，这会是全球最大NFT交
宁德时代股民年后户均亏损超百万
如何成为一名顶尖投资人？五点拿走不谢