费马小定理是数论中的一个定理。其内容为假如 a是一个整数， p是一个质数的话，那么:
a p = a(mod p)
假如 a不是 p的倍数的话，那么这个定理也可以写成:
a p − 1 = 1(mod p)
这个书写方式更加常用些。
费马小定律的广义
费马小定理是欧拉定理 (数论)的一个特殊情况：假如 n和 a的最大公约数是1的话，那么:
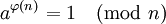
在这里φ( n)是欧拉商数。欧拉商数的值是所有小于 n的自然数中与 n没有公约数的数的量。假如 n是一个质数，则φ( n) = n-1，即费马小定理。
在费马小定理的基础上费马提出了一种测试质数的算法。
费马小定律的历史
皮埃尔·德·费马于1636年发现了这个定理，在一封1640年10月18日的信中他第一次使用了上面的书写方式。在他的信中费马还提出a是一个质数的要求。这个要求实际上不存在。
与费马无关的有一个中国猜想。这个猜想是中国数学家提出来的。其内容为如果，而且只有当2 p = 2( m o d p)成立时p才是一个质数。
假如p是一个质数的话，则2 p = 2( m o d p)成立（这是费马小定理的一个特殊情况）是对的。但反过来，假如2 p = 2( m o d p)成立那么p是一个质数是不成立的（比如341符合上述条件但不是一个质数）。因此整个来说这个猜想是错误的。
一般认为中国数学家在费马前2000年的时候就已经认识中国猜测了。但也有人认为实际上中国猜测是1872年提出的，认为它早就为人所知是出于一个误解。
费马小定律的证明
若n不整除a-b，x>0，(x,n)=1，則n也不整除x(a-b)。取整數A为所有小於p的集（p不整除A），B为A中所有元素乘以a的集合。因任何两个A中的元素差都不能被p整除，所以任何两个B中的元素差也无法被p整除。因此:
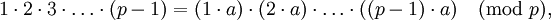
即:
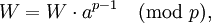
在这里 W=1·2·3·...·( p-1)。将整个公式除以 W即得到:
a p − 1 = 1(mod p)
费马小定律的的实际应用
如上所述，中国猜测只有一半是正确的，符合中国猜测但不是质数的数被称为伪质数。
假如所有符合1
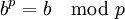
则 p必定是一个质数。
实际上没有必要测试所有的小于 p的自然数，只要测试所有的小于 p的质数就可以了。
这个算法的缺点是它非常慢，运算率高。
相关条目费马大定理
-
相关文章
刘霆龙12.10黄金走势空头能否延续
元宇宙到底是什么？这十点看完就明白了
蚂蚁链“粉丝粒”，这会是全球最大NFT交
宁德时代股民年后户均亏损超百万
如何成为一名顶尖投资人？五点拿走不谢